S h a p e o f s u r f a c e z(x,y) i n n e i g h b o u r h o o d o f a p o i n t.
Recommended prerequisites.
--------------------------
Matrix, partial derivative, intergration in |R.
Level: college entry level.
The Problem.
------------
One of the ways to describe surfaces in 3-dimentional space, is to use smooth functions of
form z(x,y). We will set aside forms of poetrical descriptions and will focus on how
such functions look in neighbourhood of a single point p0=(x0,y0).
Intuitively, if we take enough good microsope, the picture will be a flat plane.
Indeed, human probably will consider the Earth flat untill is able to observe neighbourhood
large enough. When deviations from "flattness" becomes noticeble, what shape can they take?
We'll try to sketch the problem intuitively and then make a proof.
Intuitive Sketch.
-----------------
1. If Z has second patial derivatives which are continuous in neighbourhood of p0, then
Z = Z0 + LiXi + FijXiXj + o(X)X2 (1)
Summation via equal indices is assumed: for example, LiXi = L1X1+L2X2.
We denote X1=x, X2=y.
o(X) -> 0 when X -> 0.
2. Z = Z0 + LiXi is a plane. We see it when neglect other members in (1).
3. Function S(X,X)=FijXiXj gives us first hills.
How do they look?
Matrix || Fij || has form:
|| Fij || =
|| A B ||
|| || (2)
|| B C ||
because mixed derivatives are equal.
and value S(X,X) is a scalar product:
S(Y,X) = (Y, F(X)) where Y=X.
where we denoted the vector FijXj as F(X).
We must focus on anatomy of function F.
Further, we will omit parenthesises: FX = F(X).
Note, if by accident B=0, then F simpy multiplies basis vectors by numbers
A and C. In this case,
S = AX12 + CX22. (3)
and clearly, S is a contribution of two parabolas.
If both parabolas have their horns up, then S - is elliptic paraboloid and
has minimum in point 0.
The other cases are displayed:
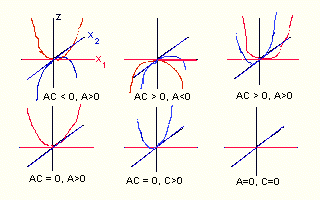 In other words, the picture depends on product AC and and sign of components.
But even if we are not so lucky in our choice of the basis, do proper vectors
exist in general case? (Vector is called proper vector of function F if "F
multiplies this vector by a number".)
Let's look at the structure of F closer.
Even matrix (2) is symmetirc, it still hides two matrices with even more symmetries.
Although in general A is not equal C, we can overcome this obstacle by letting:
D=(A-C)/2, M = (A+C)/2
which gives
|| Fij || = || Hh || + || Ht ||
where
|| Hh || = || M 0 || and || Ht || = || D B ||
|| 0 M || || B -D ||
So far, we see that function F is a contribution of two functions
F = Hh + Ht
Hh is simply a homogeneous dilation of all space by M, and "non-homogeneous" Ht is of unknown nature yet.
Matrix of || Ht || resembles matrix of rotation: || Tf || =
|| Cos(f) -Sin(f) ||
|| ||
|| Sin(f) Cos(f) ||
Indeed, we can choose G, and g:
B = GCos(g)
D = GSin(g)
that
Ht = GRTg
where || R || = || 0 1 || - is a reflection in respect to of axis X1=X2.
|| 1 0 ||
In other words, the picture depends on product AC and and sign of components.
But even if we are not so lucky in our choice of the basis, do proper vectors
exist in general case? (Vector is called proper vector of function F if "F
multiplies this vector by a number".)
Let's look at the structure of F closer.
Even matrix (2) is symmetirc, it still hides two matrices with even more symmetries.
Although in general A is not equal C, we can overcome this obstacle by letting:
D=(A-C)/2, M = (A+C)/2
which gives
|| Fij || = || Hh || + || Ht ||
where
|| Hh || = || M 0 || and || Ht || = || D B ||
|| 0 M || || B -D ||
So far, we see that function F is a contribution of two functions
F = Hh + Ht
Hh is simply a homogeneous dilation of all space by M, and "non-homogeneous" Ht is of unknown nature yet.
Matrix of || Ht || resembles matrix of rotation: || Tf || =
|| Cos(f) -Sin(f) ||
|| ||
|| Sin(f) Cos(f) ||
Indeed, we can choose G, and g:
B = GCos(g)
D = GSin(g)
that
Ht = GRTg
where || R || = || 0 1 || - is a reflection in respect to of axis X1=X2.
|| 1 0 ||
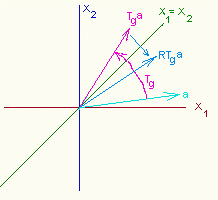 In other words, non-homogeneous part of any symmetric matrix of dimension 2 is a "rotation, swap, and dilation".
It is clear now, that we can take basis vector e1' that RTge1'=e1':
e1' = Tfe1 where f=PI/4-g/2.
Any other unit vector, e2', which is perpendicular to e1' will only change a direction when
transformation Ht is applied to it. This is because that reflection R changes direction
of the angle between two vectors, but keeps this angle's magnitude.
Hte2' = -Ge2'
In other words, non-homogeneous part of any symmetric matrix of dimension 2 is a "rotation, swap, and dilation".
It is clear now, that we can take basis vector e1' that RTge1'=e1':
e1' = Tfe1 where f=PI/4-g/2.
Any other unit vector, e2', which is perpendicular to e1' will only change a direction when
transformation Ht is applied to it. This is because that reflection R changes direction
of the angle between two vectors, but keeps this angle's magnitude.
Hte2' = -Ge2'
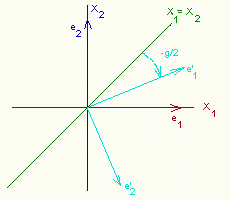 Summarizing the behavior of these two proper vectors:
Fe1' = (M+G)e1'
Fe2' = (M-G)e2'
For an arbitrary vector X = X1'e1'+X2'e2', F(X)=(M+G)X1'e1' + (M-G)X2'e2'.
S(X,X) = A'X1'2 + C'X2'2 (3').
where A'= M+G, C'=M-G.
Our parameter for shape of S can be written now as
A'C' = M2 - G2 = (A+C)(A+C)/4 - (A-C)(A-C)/4 - BB = AC-BB.
From 3', it is clear that: (4)
AC-BB > 0 and C < 0, then S is elliptic paraboloid and p is minimum of S.
AC-BB > 0 and C > 0, then S is elliptic paraboloid and p is maximum of S.
AC-BB < 0, then S is elliptic saddle.
AC-BB = 0, then at least along some line Xi' = 0 S = const.
Proof.
------
We sketched all the parts of proof except (1) which is well known.
Here is a brief ...
Proof of (1).
Z(X) = Z(b) = Z(0) + Z(a)-Z(0) + Z(b)-Z(a)
X=(X1,X2)
Axis Z is perpendicular to this picture:
0
------------> axis X2
|
|q
|
| p
|----------- b
|a
|
V
axis X1
From mean value theorem:
Za-Zo = Z1(q)X1 Z1= dZ/dX1.
Zb-Za = Z2(p)X2
q = o'(X)
p = o''(X)
p,q -> 0 when X-> 0 and
Fi(X) -> Fi(0) because of continuity of Fi.
Here and further, we will omit "(0)" at function letters for brevity: for example Z2
will denote Z2(0).
Threfore, Z(X) = Z + ZiXi + oi(X)Xi.
Applying this result to X1-derivative:
Z1(X) = Z1 + Z1jXj + o1j(X)Xj and integrating through path 0-a-b, obtain:
Z(X) = Z + Z1X1 + (Z11X1^2)/2 +
Z2X2 + (Z22X2^2)/2 + Z21X2X1 + (integral o to a)(o11X) + (integral a to b)(o21X1 + o22X2) (I)
Sum of above integrals is oI(X)XX. (1.a)
Analogiously, integrating through 0-b-a
Z(X) = Z + ZiXi + (ZiiXi^2)/2 + Z12X1X2 + oII(X)XX (II)
Comparing (I)=(II) when X1=X2<>0:
Z12 + oI = Z21 + oII.
Taking limit X1->0 we can prove that Z12 = Z21.
Adding two equations together:
Z(X) = ((I)+(II))/2 = Z + ZiXi + (1/2)ZijXij + (oI+oII)XX
which completes proof of (1) if to take Fij = (1/2)Zij.
Remaining proofs for (3)-(4) will follow if time permits. They are already sketched with enough details.
Terminology:
------------
Elliptical paraboloid: http://en.wikipedia.org/wiki/Paraboloid
Copyright (C) 2008 Konstantin Kirillov.
Summarizing the behavior of these two proper vectors:
Fe1' = (M+G)e1'
Fe2' = (M-G)e2'
For an arbitrary vector X = X1'e1'+X2'e2', F(X)=(M+G)X1'e1' + (M-G)X2'e2'.
S(X,X) = A'X1'2 + C'X2'2 (3').
where A'= M+G, C'=M-G.
Our parameter for shape of S can be written now as
A'C' = M2 - G2 = (A+C)(A+C)/4 - (A-C)(A-C)/4 - BB = AC-BB.
From 3', it is clear that: (4)
AC-BB > 0 and C < 0, then S is elliptic paraboloid and p is minimum of S.
AC-BB > 0 and C > 0, then S is elliptic paraboloid and p is maximum of S.
AC-BB < 0, then S is elliptic saddle.
AC-BB = 0, then at least along some line Xi' = 0 S = const.
Proof.
------
We sketched all the parts of proof except (1) which is well known.
Here is a brief ...
Proof of (1).
Z(X) = Z(b) = Z(0) + Z(a)-Z(0) + Z(b)-Z(a)
X=(X1,X2)
Axis Z is perpendicular to this picture:
0
------------> axis X2
|
|q
|
| p
|----------- b
|a
|
V
axis X1
From mean value theorem:
Za-Zo = Z1(q)X1 Z1= dZ/dX1.
Zb-Za = Z2(p)X2
q = o'(X)
p = o''(X)
p,q -> 0 when X-> 0 and
Fi(X) -> Fi(0) because of continuity of Fi.
Here and further, we will omit "(0)" at function letters for brevity: for example Z2
will denote Z2(0).
Threfore, Z(X) = Z + ZiXi + oi(X)Xi.
Applying this result to X1-derivative:
Z1(X) = Z1 + Z1jXj + o1j(X)Xj and integrating through path 0-a-b, obtain:
Z(X) = Z + Z1X1 + (Z11X1^2)/2 +
Z2X2 + (Z22X2^2)/2 + Z21X2X1 + (integral o to a)(o11X) + (integral a to b)(o21X1 + o22X2) (I)
Sum of above integrals is oI(X)XX. (1.a)
Analogiously, integrating through 0-b-a
Z(X) = Z + ZiXi + (ZiiXi^2)/2 + Z12X1X2 + oII(X)XX (II)
Comparing (I)=(II) when X1=X2<>0:
Z12 + oI = Z21 + oII.
Taking limit X1->0 we can prove that Z12 = Z21.
Adding two equations together:
Z(X) = ((I)+(II))/2 = Z + ZiXi + (1/2)ZijXij + (oI+oII)XX
which completes proof of (1) if to take Fij = (1/2)Zij.
Remaining proofs for (3)-(4) will follow if time permits. They are already sketched with enough details.
Terminology:
------------
Elliptical paraboloid: http://en.wikipedia.org/wiki/Paraboloid
Copyright (C) 2008 Konstantin Kirillov.
 In other words, the picture depends on product AC and and sign of components.
But even if we are not so lucky in our choice of the basis, do proper vectors
exist in general case? (Vector is called proper vector of function F if "F
multiplies this vector by a number".)
Let's look at the structure of F closer.
Even matrix (2) is symmetirc, it still hides two matrices with even more symmetries.
Although in general A is not equal C, we can overcome this obstacle by letting:
D=(A-C)/2, M = (A+C)/2
which gives
|| Fij || = || Hh || + || Ht ||
where
|| Hh || = || M 0 || and || Ht || = || D B ||
|| 0 M || || B -D ||
So far, we see that function F is a contribution of two functions
F = Hh + Ht
Hh is simply a homogeneous dilation of all space by M, and "non-homogeneous" Ht is of unknown nature yet.
Matrix of || Ht || resembles matrix of rotation: || Tf || =
|| Cos(f) -Sin(f) ||
|| ||
|| Sin(f) Cos(f) ||
Indeed, we can choose G, and g:
B = GCos(g)
D = GSin(g)
that
Ht = GRTg
where || R || = || 0 1 || - is a reflection in respect to of axis X1=X2.
|| 1 0 ||
In other words, the picture depends on product AC and and sign of components.
But even if we are not so lucky in our choice of the basis, do proper vectors
exist in general case? (Vector is called proper vector of function F if "F
multiplies this vector by a number".)
Let's look at the structure of F closer.
Even matrix (2) is symmetirc, it still hides two matrices with even more symmetries.
Although in general A is not equal C, we can overcome this obstacle by letting:
D=(A-C)/2, M = (A+C)/2
which gives
|| Fij || = || Hh || + || Ht ||
where
|| Hh || = || M 0 || and || Ht || = || D B ||
|| 0 M || || B -D ||
So far, we see that function F is a contribution of two functions
F = Hh + Ht
Hh is simply a homogeneous dilation of all space by M, and "non-homogeneous" Ht is of unknown nature yet.
Matrix of || Ht || resembles matrix of rotation: || Tf || =
|| Cos(f) -Sin(f) ||
|| ||
|| Sin(f) Cos(f) ||
Indeed, we can choose G, and g:
B = GCos(g)
D = GSin(g)
that
Ht = GRTg
where || R || = || 0 1 || - is a reflection in respect to of axis X1=X2.
|| 1 0 ||
 In other words, non-homogeneous part of any symmetric matrix of dimension 2 is a "rotation, swap, and dilation".
It is clear now, that we can take basis vector e1' that RTge1'=e1':
e1' = Tfe1 where f=PI/4-g/2.
Any other unit vector, e2', which is perpendicular to e1' will only change a direction when
transformation Ht is applied to it. This is because that reflection R changes direction
of the angle between two vectors, but keeps this angle's magnitude.
Hte2' = -Ge2'
In other words, non-homogeneous part of any symmetric matrix of dimension 2 is a "rotation, swap, and dilation".
It is clear now, that we can take basis vector e1' that RTge1'=e1':
e1' = Tfe1 where f=PI/4-g/2.
Any other unit vector, e2', which is perpendicular to e1' will only change a direction when
transformation Ht is applied to it. This is because that reflection R changes direction
of the angle between two vectors, but keeps this angle's magnitude.
Hte2' = -Ge2'
 Summarizing the behavior of these two proper vectors:
Fe1' = (M+G)e1'
Fe2' = (M-G)e2'
For an arbitrary vector X = X1'e1'+X2'e2', F(X)=(M+G)X1'e1' + (M-G)X2'e2'.
S(X,X) = A'X1'2 + C'X2'2 (3').
where A'= M+G, C'=M-G.
Our parameter for shape of S can be written now as
A'C' = M2 - G2 = (A+C)(A+C)/4 - (A-C)(A-C)/4 - BB = AC-BB.
From 3', it is clear that: (4)
AC-BB > 0 and C < 0, then S is elliptic paraboloid and p is minimum of S.
AC-BB > 0 and C > 0, then S is elliptic paraboloid and p is maximum of S.
AC-BB < 0, then S is elliptic saddle.
AC-BB = 0, then at least along some line Xi' = 0 S = const.
Proof.
------
We sketched all the parts of proof except (1) which is well known.
Here is a brief ...
Proof of (1).
Z(X) = Z(b) = Z(0) + Z(a)-Z(0) + Z(b)-Z(a)
X=(X1,X2)
Axis Z is perpendicular to this picture:
0
------------> axis X2
|
|q
|
| p
|----------- b
|a
|
V
axis X1
From mean value theorem:
Za-Zo = Z1(q)X1 Z1= dZ/dX1.
Zb-Za = Z2(p)X2
q = o'(X)
p = o''(X)
p,q -> 0 when X-> 0 and
Fi(X) -> Fi(0) because of continuity of Fi.
Here and further, we will omit "(0)" at function letters for brevity: for example Z2
will denote Z2(0).
Threfore, Z(X) = Z + ZiXi + oi(X)Xi.
Applying this result to X1-derivative:
Z1(X) = Z1 + Z1jXj + o1j(X)Xj and integrating through path 0-a-b, obtain:
Z(X) = Z + Z1X1 + (Z11X1^2)/2 +
Z2X2 + (Z22X2^2)/2 + Z21X2X1 + (integral o to a)(o11X) + (integral a to b)(o21X1 + o22X2) (I)
Sum of above integrals is oI(X)XX. (1.a)
Analogiously, integrating through 0-b-a
Z(X) = Z + ZiXi + (ZiiXi^2)/2 + Z12X1X2 + oII(X)XX (II)
Comparing (I)=(II) when X1=X2<>0:
Z12 + oI = Z21 + oII.
Taking limit X1->0 we can prove that Z12 = Z21.
Adding two equations together:
Z(X) = ((I)+(II))/2 = Z + ZiXi + (1/2)ZijXij + (oI+oII)XX
which completes proof of (1) if to take Fij = (1/2)Zij.
Remaining proofs for (3)-(4) will follow if time permits. They are already sketched with enough details.
Terminology:
------------
Elliptical paraboloid: http://en.wikipedia.org/wiki/Paraboloid
Copyright (C) 2008 Konstantin Kirillov.
Summarizing the behavior of these two proper vectors:
Fe1' = (M+G)e1'
Fe2' = (M-G)e2'
For an arbitrary vector X = X1'e1'+X2'e2', F(X)=(M+G)X1'e1' + (M-G)X2'e2'.
S(X,X) = A'X1'2 + C'X2'2 (3').
where A'= M+G, C'=M-G.
Our parameter for shape of S can be written now as
A'C' = M2 - G2 = (A+C)(A+C)/4 - (A-C)(A-C)/4 - BB = AC-BB.
From 3', it is clear that: (4)
AC-BB > 0 and C < 0, then S is elliptic paraboloid and p is minimum of S.
AC-BB > 0 and C > 0, then S is elliptic paraboloid and p is maximum of S.
AC-BB < 0, then S is elliptic saddle.
AC-BB = 0, then at least along some line Xi' = 0 S = const.
Proof.
------
We sketched all the parts of proof except (1) which is well known.
Here is a brief ...
Proof of (1).
Z(X) = Z(b) = Z(0) + Z(a)-Z(0) + Z(b)-Z(a)
X=(X1,X2)
Axis Z is perpendicular to this picture:
0
------------> axis X2
|
|q
|
| p
|----------- b
|a
|
V
axis X1
From mean value theorem:
Za-Zo = Z1(q)X1 Z1= dZ/dX1.
Zb-Za = Z2(p)X2
q = o'(X)
p = o''(X)
p,q -> 0 when X-> 0 and
Fi(X) -> Fi(0) because of continuity of Fi.
Here and further, we will omit "(0)" at function letters for brevity: for example Z2
will denote Z2(0).
Threfore, Z(X) = Z + ZiXi + oi(X)Xi.
Applying this result to X1-derivative:
Z1(X) = Z1 + Z1jXj + o1j(X)Xj and integrating through path 0-a-b, obtain:
Z(X) = Z + Z1X1 + (Z11X1^2)/2 +
Z2X2 + (Z22X2^2)/2 + Z21X2X1 + (integral o to a)(o11X) + (integral a to b)(o21X1 + o22X2) (I)
Sum of above integrals is oI(X)XX. (1.a)
Analogiously, integrating through 0-b-a
Z(X) = Z + ZiXi + (ZiiXi^2)/2 + Z12X1X2 + oII(X)XX (II)
Comparing (I)=(II) when X1=X2<>0:
Z12 + oI = Z21 + oII.
Taking limit X1->0 we can prove that Z12 = Z21.
Adding two equations together:
Z(X) = ((I)+(II))/2 = Z + ZiXi + (1/2)ZijXij + (oI+oII)XX
which completes proof of (1) if to take Fij = (1/2)Zij.
Remaining proofs for (3)-(4) will follow if time permits. They are already sketched with enough details.
Terminology:
------------
Elliptical paraboloid: http://en.wikipedia.org/wiki/Paraboloid
Copyright (C) 2008 Konstantin Kirillov.