If Greek characters are not displayed properly,
reader should enable them on reader's browser or
find browser which supports charset iso-8859-7
Slow computers may not display animation well.
Let's consider Lorentz Transformation (if to choose system of units where light speed = 1)
T = â(t - vx )
X = â(-vt + x)
where as usual â = 1 / ( 1 - v
2
)1/2
v - is a speed of inertial system K which moves along axis x of the system "at rest" k;
x,t are measured in k;
X,T are measured in K.
The function
ó = t
2
- x
2
.
has notable property:
Ó = ó
where Ó = T
2
- X
2
.
In other words, points T(X) representing the same event
will form contour of function Ó or solution of equation:
T
2
- X
2
= const
For example, if to choose an event (t,x) which happened at the time t at origin of the
system "at rest" x=A,
and then consider this event in all inertial systems which move
along axis x,
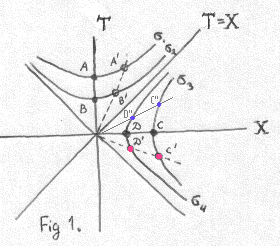
then the graph T(X) of such events will form "hyperbola"
with minimum at X=A and asymptotes T=X and T=-X.
Using substitution method, it can be checked that Lorentz Transformation does not chage a shape
of group of events which belong one line. In other words, line t(x) = ax + b transforms to line also.
So, events which lie on axis x happen simultaneously (like events D and C ), but at certain v this line
transforms to a line D'C' with neither of its events happened simultaneously because they
have different ordinates.
Moreover, events lying on line D'' C'' have different time order when they observed in
system where they presented by line D' C'. For example, event D'' happened "before" event C'', but
the same event D' happened "after" event C'.
More details about Fig. 1.
Events A happened after event B in system k. They both happened at origin x=0.
When we imagine sequence of inertial systems with decreasing speed v,
then point A moves along the
right branch of hyperbola ó1;
point B moves along hyperbola ó2.
For example, if v < 0 then, event A viewed in system K, will be represented by point A'.
The same way, it is easy to verify that event D moves along the down branch of hyperbola
D, D'.